What Do Onion Skins and Zebra Strips Have in Common? New Geometric Shapes Identified by BME Mathematicians

Geometric shapes can be found in several tissues in nature, such as muscle cells, the shell of the chambered nautilus or even the epithelial cells covering the inside of organs, that have inspired researchers to make a new scientific discovery. For a long time, it was a mystery how these “soft shapes”, as they are called, evolved in nature but not long ago Hungarian mathematicians in an international collaboration have found the answer, and their discovery was recently published in the prestigious PNAS Nexus journal.

Participants in the work were Gábor Domokos (architect, applied mathematician, leader of the HUN- REN-BME Morphodynamics of Solids Research Group, research professor at the BME Department of Morphology and Geometric Modeling), Krisztina Regős, (PhD student at the BME Faculty of Architecture, member of HUN-REN-BME Morphodynamics of Solids Research Group), Ákos G. Horváth (head of department of and university professor at the Department of Algebra and Geometry of Institute of Mathematics of BME Faculty of Natural Sciences, member of HUN-REN-BME Morphodynamics of Solids Research Group) and Alain Goriely (professor of applied mathematics at Oxford University).

No gaps or overlaps

‘Ever since Plato’s theory, which identified the elements with regular polyhedra, mathematicians have been interested in space-filling tilings, in other words, shapes that cover the plane or fill the available space without gaps or overlaps. Triangles and other polygons are commonly studied as space-filling shapes in the plane, and cubes and other polyhedra in space, but these have sharp vertices, straight edges or flat faces rarely seen in living organisms. Evolution has rather produced space-filling shapes with strongly curved edges, curved surfaces and few, sometimes zero, sharp corners, coposed of such forms,’ explains Gábor Domokos the background of the discovery.

The softly shaped truncated octahedron.

According to the professor, soft cells have curved edges and two vertices in the plane. Such patterns can be found, for example, in plane sections of muscle tissue, in zebra stripes, in the shapes of river islands, in onion layers and even in architectural design.

In three dimensions, however, the situation becomes more complicated, as soft cells in space do not have a vertex. Researchers at the BME working on the topic have developed a procedure in which based on a known polyhedron (sharp) pattern (e.g. a cubic grid) a space filling made up of soft cells has been created by deforming the edges properly. Using this procedure, several types of soft cells were identified. (The procedue is illustrated in the animated video below:

After drawing their conclusions, the researchers observed numerous soft cell formations in our natural and built environment. One of the most interesting case was the case of the nautilus, as the inner chambers of the nautilus shell are soft cells. Krisztina Regős from the research team had the idea that although the cross-section of chambers is a planar soft cell with two corners, they will not be vertices in space. She was right. Using detailed micro-CT images of the shell, the experts found that the chambers of the nautilus and many ammonites are soft cells that fill the outer shell without corners.

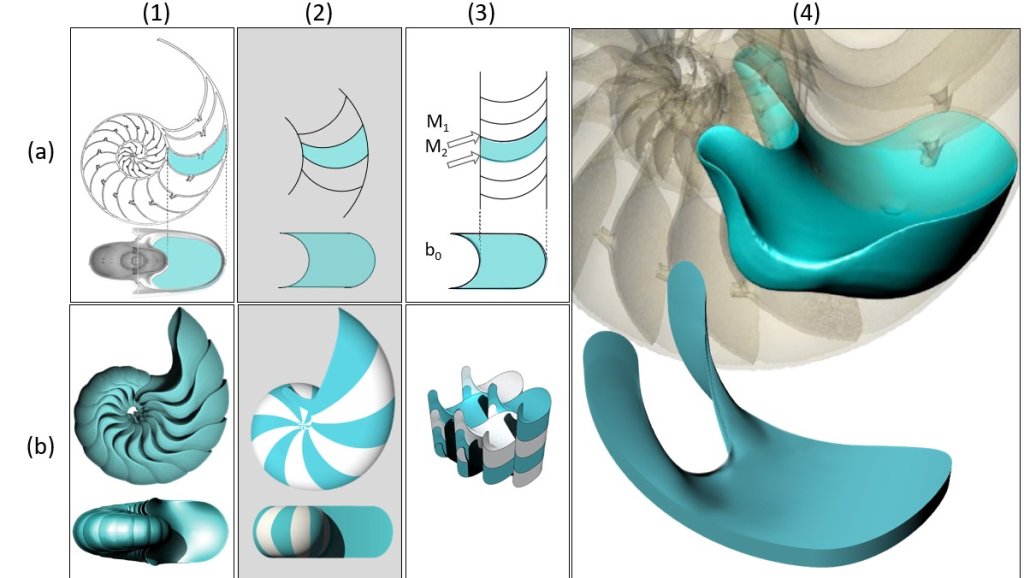
Geometric model of the Nautilus. Right: comparison of the Nautilus cell and the mathematical model

The geometric discovery suggests that soft cells are the geometric building blocks of biological tissues. With the new model, experts can now describe why different patterns form and grow in living tissue and why nature prefers them.

A deeper understanding of soft cells could explain, for example, the static geometry of tissues or even one of the most common biological processes of shape evolution, the growth of plant roots.

The preprint version of the publication of the recent discovery has attracted the interest of the international academic world. Several scientific journals contacted Gábor Domokos, reported the main findings of the discovery, and the news reached some architecture students at the California College of Arts, who built a creative project based on the Hungarian experts' theory. Their soft cell design won the science prize of the biodesign competition both at the Parsons School in New York, which is the world's most prestigious design school, and at the Museum of Modern Arts.

According to Gábor Domokos, the application possibilities of a new geometric construction is often only emerge long after the publication, and this was also noticable in the case of the Gömböc. As for the soft cells, mathematical questions, biological and architectural applications are already emerging, but it is possible that new scientific evidences in other areas will join the discovery in time.

TZS

Photo sources: Lajos Czeglédi, Gábor Domokos, Krisztina Regős