„Bemutatni a fiataloknak, hogy a matematikának ’varázsereje’ van”

Függvényekről, a matematika egyik alapfogalmáról és történeti érdekességekről szólt Molnár Lajos matematikus előadása a Science Campus rendezvénysorozat keretében.

„A függvény a matematika tudományának egyik központi fogalma, amellyel minden középiskolás találkozik valamilyen formában a tanulmányai során. Természettudományos általános műveltségünk része, ám a fiatalok középfokú tanulmányaikban kevés tapasztalatot, ismeretet szerezhetnek arról, milyen szerteágazó lehetőségeket magában rejtő matematikai fogalomról van szó, amely számos kutatás alapja volt és az ma is” – foglalta össze „Furcsa függvények” címmel tartott előadásának bevezetésében Molnár Lajos matematikus, a BME Természettudományi Kar Matematika Intézet Analízis Tanszékének egyetemi tanára, aki e rendkívül fontos fogalom rejtelmeibe vezette be a Science Campus előadássorozat résztvevőit.

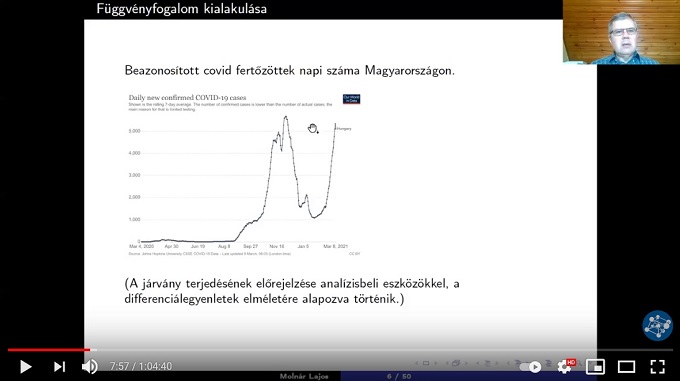
„A mai középiskolai tankönyvekben szereplő meghatározás a következő: ha adott két halmaz, A és B, és az A halmaz minden eleméhez hozzárendeljük a B halmaz valamely elemét, akkor ezt a hozzárendelést függvénynek nevezzük” – kezdte Molnár Lajos, aki előadásának első részében áttekintést adott a függvény fogalmának kialakulásáról és több száz éves formálódásáról. „A mindennapi életben is lépten-nyomon találkozhatunk függvényekkel, amelyek közül talán a legnagyobb figyelem mostanában az életünket az elmúlt másfél évben jelentős mértékben befolyásoló, napi új COVID-vírussal fertőzöttek számát megadó függvényt övezte” – hozott fel egy népszerű példát az egyetemi oktató, majd hangsúlyozta, hogy a függvények tanulmányozása a klasszikus matematikai analízis területének központi kérdése. „A járvány elleni védekezésben fontos szerepet játszott a matematikai analízis egyik ágának, a differenciálegyenletek elméletének eredményein alapuló járványterjedési modellek használata.”

Molnár Lajos előadásában a valós számokhoz valós számokat rendelő függvényekre vonatkozó két alapvető, bizonyos értelmű regularitási tulajdonsággal foglalkozott: a folytonossággal és a differenciálhatósággal lokális és globális értelemben.

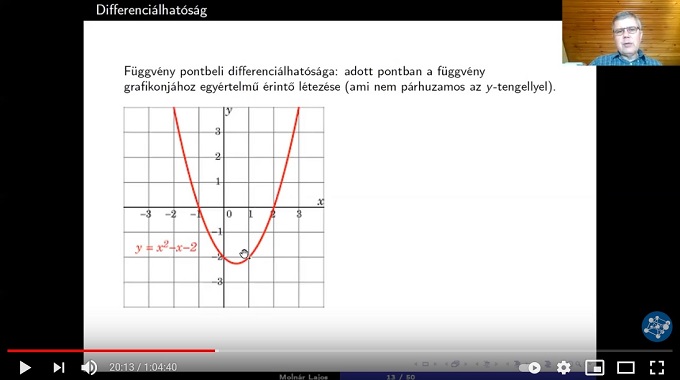
„Mindkét tulajdonsággal kapcsolatban az emberek többségében él egy szemléletes kép. Folytonosnak tartunk egy függvényt, ha grafikonjának megrajzolása során nem kell ’felemelnünk’ az íróeszközt. Egy függvényt pedig differenciálhatónak mondunk egy pontban, ha ott ’nem törik meg’, grafikonjához egyértelmű érintő húzható. Természetesen mindkét tulajdonságnak megvan a szigorú, pontos matematikai definíciója is” – mondta a TTK matematikusa és kiemelte: az előadásban bemutatott „fura függvények” jól példázzák, hogy a szemléletre alapozott megérzések esetenként nagyon távol állnak a tudományos igazságtól.

Molnár Lajos a függvények folytonosságával kapcsolatban felvetette a kérdést, hogy mennyire lehet nem folytonos, hány helyen „szakadhat” egy függvény. A hallgatóság számára meglepő válasz: akár mindent pontban, amelyre Dirichlet mutatott rá 1829-ben.

Hasonló kérdést vizsgált a differenciálhatóságra vonatkozóan is: hány helyen „törhet meg” egy folytonos függvény, amire a válasz az előzőleg felvetett kérdéshez hasonlóan: akár minden pontban. Ilyen függvényre az első publikált példát 1872-ben Weierstrass közölte, akinek felfedezését kora matematikusainak többsége nagy megdöbbenéssel fogadta. „Fontos megjegyezni, hogy Ampère kevéssel korábban még amellett érvelt, hogy egy tetszőleges folytonos függvénynek bizonyos izolált helyektől eltekintve mindenütt differenciálhatónak kell lennie. Gondolatmenete egy szemléletre alapozott, vélt tényt is használt, amiről kiderült, hogy matematikailag helytelen” – tartott újabb történeti kitekintést a műegyetemi oktató.

Előadásának folytatásában azt az izgalmas kérdést vizsgálta, hogy mennyire extrém a fenti jelenség, a sehol sem differenciálhatóság a folytonos függvények körében. Elmondása szerint kiderült, hogy egyáltalán nem extrém, sőt bármennyire is mást sugall a szemlélet, az igazság az, hogy sokkal inkább tipikusnak nevezhető. Ezzel kapcsolatos eredmények is szerepeltek az előadásban, majd Molnár Lajos arra is rámutatott, hogy a laikusok véleményével szemben, miszerint a matematika lényegében „lezárt tudomány”, sokkal inkább aktív, változó és rendszeresen megújuló tudományterület. Példaként hozta fel a folytonos sehol sem differenciálható függvényeket: annak ellenére, hogy vizsgálatuk majd másfél évszázada kezdődött, az utóbbi időben is százával születtek-születnek új tudományos eredmények a területen.

A műegyetemi oktató kutató további furcsa függvénnyel kapcsolatos ismereteket is a közönség elé tárt. Az ördög lépcsőjének is nevezik Cantor 1884-ben konstruált nevezetes függvényét. Ez egy olyan, a [0,1] intervallumot önmagára képező folytonos függvény, ami monoton növekvő, ám azon pontok halmaza, ahol ténylegesen (szigorúan) növekszik, rendkívül kicsi, bizonyos matematikai értelemben nulla mértékkel bír. Azt mondhatjuk, hogy a függvény értékei úgy növekednek folytonosan a 0 értéktől 1-ig, hogy közben a függvény lényegében mindig áll. Az előadó bemutatta, hogy az utóbbi időkben különböző tudományterületeken számos jelenség magyarázata, leírása során használnak Cantor-típusú függvényeket a tudósok. Két példa az újabbak közül: nagy földrengések időbeli lefolyásának és sorozatgyilkosok viselkedésének leírása.

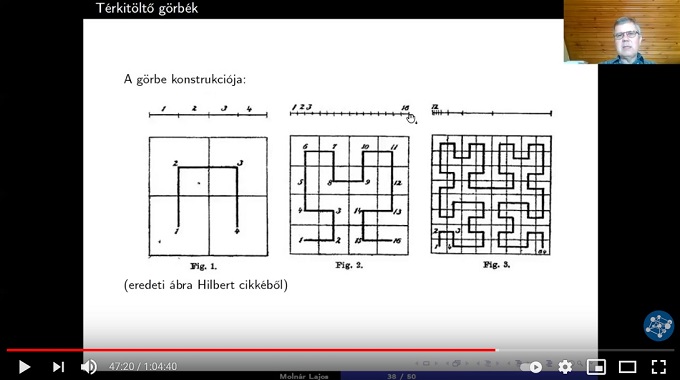
Előadása utolsó részében Molnár Lajos azt taglalta, hogy vajon ki lehet-e tölteni az egységnégyzetet folytonos görbével, be lehet-e járni annak minden pontját egy folytonos görbe mentén egységnyi idő alatt. Az egyszerű szemléletes képpel ismét ütköző válasz az, hogy igen. „Számos különböző ilyen konstrukció ismert” – jelentette ki az előadó, aki Hilbert példáját mutatta be, amit a kor matematikus fejedelme 1891-ben publikált. Az eredeti kérdés és az arra adott válasz teljesen elméleti jellegű, ám ahogy az számos esetben megtörtént már elméleti matematikai eredményekkel, hasznos gyakorlati alkalmazásra talált. Az okostelefont használók nap, mint nap kapcsolatba kerülhetnek Hilbert konstrukciójával, ugyanis ezen alapul a Google azon szolgáltatása, amit akkor veszünk igénybe, amikor egy adott hely közelében pl. éttermet keresünk. Molnár Lajos vázolta, hogyan történik a földrajzi helyek sorba rendezése, azok egy darab bináris számmal való leírására Hilbert konstrukciójára alapozva.

A Science Campus előadás utolsó perceiben újabb kitekintésként egy Esterházy Péterrel (aki egyetemi tanulmányait matematikus szakon végezte) készült interjúból hangzott el az alábbi részlet: „Amikor az első órám volt az egyetemen, a belépő professzor, köszönés helyett, így kezdte: tekintsük az ’A’ halmazt. 1968-ban jártunk, mi bevonultunk Csehszlovákiába, az apám éppen a jelentéseit írta, az öcsém ellopta a radírgumimat, és akkor valaki azzal az ajánlattal rukkol elő: tekintsük az ’A’ halmazt. Ez nyomban elvarázsolt, lenyűgözött, és mondhatni az irodalom irányába lódított, mert a regény is ’A’ halmaz, önálló világ, ahol minden létező önálló életet él, megtoldva azzal, hogy őket én teremtem.”

„A matematika más tudományok szempontjából is meghatározóan fontos volta, számos elméleti eredményének hétköznapi életben való hasznosíthatósága kétségtelen. A matematikának ezen alapvető jellemzői mellett az Esterházy Péter által említett értelemben ’varázsereje’ is van. Bízom benne, hogy valamilyen mértékben sikerült a hallgatóság, az érdeklődő középiskolások számára ezt megmutatni” – zárta a bme.hu-nak adott interjút Molnár Lajos.

TZS-HA

Fotók forrása: NKFIH, Molnár Lajos online előadása